Based on the comments in the previous post, it seems like many players generate their characters using the following method:
- Roll 4d6
- Discard the lowest number
- Add the remaining three together
- Wait until the DM isn’t looking
- Write down whatever numbers you want.
- Make sure one of them is a 9, just to keep yourself “honest”.
If you could graph these numbers, I bet they would form a very nice curve that peaks around 15.5. People are very predictable when generating “random” numbers.
But let’s look at a few more graphs of character score distributions. Just because. First, the standard character distribution. Roll 4d6 and discard the lowest. It produces the now-familiar curve.

We’ve seen that. Now, what would it look like if we just roll only three dice and just add them up?

That really brings the averages down quite a bit. The process of rolling an extra die and discarding the lowest moves scores upwards by about two full points. What if we went the other way, and rolled two extra dice, keeping only the three highest?
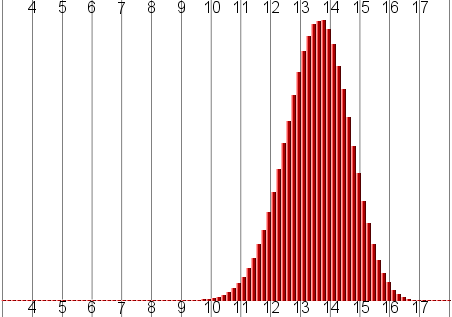
Adding an extra die moves scores up by a point. Now, try rolling twelve six-sided die, and then divide the result by four. This is basically like doing the three dice method above, except we are doing it four times and averaging the results.

It produces characters pretty much the same as the three-dice method, but the curve is much steeper. The odds against getting a weak or strong character are astronomical. Everyone is going to be more or less the same this way. I know there isn’t a nine-sided die, but what if there was? Let’s roll up our characters using 2d9.

That produces a very broad curve. In contrast to the one before it, this would give us tremendous variety in character scores. We could have even more variety by rolling a single 18-sided die for each of our stats.

This produces the broadest distribution so far, which is probably pretty realistic. It also means the average is right around 9, which is “below average” for a human being. We could correct this by rolling 2d18 and discarding the lower, but I think you get the idea by now.
Ok, I’m done with this for now.
The Gradient of Plot Holes

Most stories have plot holes. The failure isn't that they exist, it's when you notice them while immersed in the story.
Pixel City Dev Blog
An attempt to make a good looking cityscape with nothing but simple tricks and a few rectangles of light.
Secret of Good Secrets

Sometimes in-game secrets are fun and sometimes they're lame. Here's why.
Silver Sable Sucks

This version of Silver Sable is poorly designed, horribly written, and placed in the game for all the wrong reasons.
Push the Button!

Scenes from Half-Life 2:Episode 2, showing Gordon Freeman being a jerk.
 T w e n t y S i d e d
T w e n t y S i d e d
are you using MATLAB or IDL or something else? nice graphs :)
Heh. My program just spit out HTML for the graphs. In the first post I cut & pasted the HTML, but for this post I took the time to turn them into images and scale them down.
you coded your simulation in C directly? dude… awesome.
Shouldn’t you do 1d16+2 for your one-die attribute? That way you still get the 3-18 distribution, as well as keeping the average score ten and a half (the same as 3d6). Yeah, I’m old-school enough to remember when 4d6, discard lowest was an optional rule for producing stronger-than-normal characters.
3-18 for two dice is screwier, though. 2d9 is 2-18, average 10. And 2d8+2 is 4-18, average 11.
Well all our characters are allowed three sets of rolls and the player picks the best set he wants in the three.
Doing it this way gives the character the option of having some high ability scores or an average set, unless of course they roll three bad sets of stats.
My best stats are 17,18,18,13,16,18
However I have c30 characters with around 30 dead ones as well each rolled up in this method which makes c200 rolls of the dice….
Your distribution for 1d18 is off. It should be, of course, a perfectly flat distribution, with 1/18 odds of any # between 1 and 18, inclusive. If you’re getting a bell curve like that, that’s one heck of a loaded simulated die.
These aren’t the odds of rolling individual numbers. These are the average strengths of D&D characters, which have six different stats.
Basically, these are the averages you get when you roll the die/dice six times in a row and average them all out. A single roll on a D18 would have an even distribution, but six rolls averaged get a bell curve, since it’s equally likely you’ll get a low roll as you would a high one.
dan: This is the average of all character stats, not individual rolls. To roll up a character, I would roll my d18 6 times. Thus the bell curve.
Have you thought about another alternative that’s been used, namely “roll 3d6 seven times and drop the lowest number”?
I used to do both, occasionally – 4d6 seven or eight times, drop the lowest die on each roll and drop the lowest extra numbers.
What if you use the system where you roll 4d6, re-roll any ones, then discard the lowest number and add the rest up?
It gives my group fairly strong characters, with no-one having a score less than 6.(Good for high powered campains.) The average roll seems to be abot 14 or 15.
In my next campaign, I’m considering using what the designers called the “Organic Method”:
1. Roll 4d6, discarding the lowest die. Do this six times (naturally), but keep the results in the order rolled.
2. If desired, select one number and roll again. If the second result is higher, use it instead of the original.
3. If desired, exchange any two results.
4. Record these in order of Strength, Dexterity, Constitution, etc.
I imagine it might be possible to craft some sort of bell-curve for this one, if you go with the assumption that the seventh roll (the one that tries to replace one) is done against the lowest number. I have no idea how to go about calculating this, though.
‘Course, I’ve been using a point-buy method for the last couple years, but I’m getting kinda tired of everyone in the group essentially having the same stats.
I have a story that kinda goes with this…
I was rolling up characters today, ’cause I was bored, and then choosing a race for them. One of the four I rolled up had 3 CHA, and I didn’t look at the racial penalty for dwarves…
So that character has 1 CHA, and I’m now lots of fun speculating why. Thing is, all his other scores were at least 13, without bonuses, so obviously he’s strong, smart, agile, but extremely unlikable. Grumpy? Ugly? Both? I’ll have to decide…
I suggest (two years later, which I’m sure is going to be useful) arrogant.
Or possibly just socially messed up. Shy, autistic, unable to connect, that sort of thing.
Man, the future is awesome. Too bad the other people in this comment thread aren’t there yet.
My first DM did it like this:
1) Roll your three dice. Seven times. Discard the lowest one! This *almost* always eliminates your one unlucky eight or nine, though we had one guy who managed to roll a three, five, and nine on one character.
2) If you’ve got pesky odd numbers and want to either grab that extra bonus or avoid a penalty on another stat, shift a point.
He also showed us the roll-four-keep-three trick, which was interesting, but I don’t recall using it.
My group decided that we didn’t want to play characters any where close to avergae people so we use these rules:
1) roll 5d6 drop the low two
2) reapet untill you have seven scores
3) pick the 5 highest
4) add an 18
5) arrange as desired
It makes way over powered characters but that’s the point of the game right? To get as awesome as possible?
You should not average per all stats as you and dan hashed out… you should find the prob. for each stat individually. What good is it saying that 1d6 has a bell curve on the 3.5?…. thats why your graphs are so screwed up… for in fact, the bell curve that you claim is all too familiar- looks nothing like the familiar bell curve. I do recall getting 17’s 18’s and many low rolls as well and not infrequently. Although as that graph would have it, the chance of getting a 17 is almost nonexistent. All that (including all 6) did, was make the bell curves 6 times more radical. Which is helpful if you intend to roll 6 times per stat but that isn’t the case here. I recognize you are finding the avg. stat of a system but that will happen whether or not you make the results 6 times more radical…. provided the chances aren’t equal (but people can calculate what half of a number is on their own) and on top of that… you get to see what (on avg.) your chances are for rolling each individual stat are. I just cant see the benefit in doing it this way.
When I was a wee young’un who mostly just watched my old man’s D&D (AD&D2) group, the rolling process they had was weighted to both keep things average, but to increase the chance of outliers. Generally, they rolled 3d6 + 1d8, and dropped the lowest, capping at 18. It slightly increased the chances of rolling higher scores while still keeping the majority of attributes within an average range.
I wonder what the results would be on this scale, though I recognize the algorithm would likely need to change a wee bit to accomodate having 2 different types of dice. The one other thing they did was they would allow a double-roll, and you could pick which of the two sets of scores you felt was better for your character. this could skew the numbers slightly towards a higher average, but with the same averages along the whole way, I expect the effects of this second part would be fairly small compared to the changing of 1d6 to 1d8.
How about letting the players suggest a method they “think is fair”. Use those words and lay out how you just want average characters. Then give everyone the inverse. It’s all random right? right?
Might keep em honest in the future!
Roll 6d20, three times. Pick the best.
Extreme stats – high or low – are always more fun to play.
So with your recent link to the previous post in this series, I tried a little code experiment (using WPF and C# Parallel.For as an experiment) and rolled 100 billion characters. Interestingly it did almost exactly 1 million iterations per second (i.e. 1 billion iterations took 996 seconds)
My highest score was 17.7 (being composed of 18, 18, 18, 16, 18) on iteration 75012350201 and lowest was 5.2 (4,7,4,6,4,6) on iteration 865027029.
My first attempt at running I was logging all of the results, but my computer didn’t like the idea of a 13TB file very much, so I changed to only recording the max / min achieved.